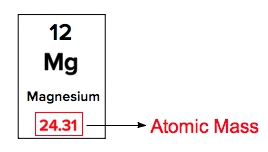
Atomic Mass (Simplified) - Video Tutorials & Practice Problems

Atomic Mass (Conceptual) Concept 1

atomic masses of elements can be found by simply looking at the periodic table. So let's start off by looking at the symbol of H, which represents hydrogen. And if you take a look at hydrogen as well as the other elements on the periodic table, you'll see these whole numbers. These whole numbers represent our atomic number. They are the number of protons. When we say atomic mass. Though the atomic mass is the number that is seldom a whole number, this is our atomic mass. So you can find the atomic mass of any element on the periodic table. Just by simply looking it up. Now we're gonna say the atomic mass itself is an average of all its isotopes that use the units of grams per mole am you or dalton's. And we're going to say remember that one a.m. U. Equals 1.66 times 10 to the negative kg. So just remember these atomic masses that you see on the periodic table. They are usually not whole numbers. You'd have to get way down below here to these heavy elements down here. So you see whole numbers for atomic masses. And remember they are the average of all the isotopes for that given element

Atomic Mass (Conceptual) Example 1

So here for this example question it says which of the following represents an element from the first column with the greatest atomic mass. Alright, so our first column, if we look at this periodic table, our first column is this with all of these different elements. And remember the number in red? Which is not a whole number. Normally that represents the atomic mass of any of these given elements. Now here, if we take a look we have barium, be a again later we'll learn about how the names are attached to the element symbol B A is not in the first column here, it's in the second column. So this cannot be a choice then we're gonna say next that we have A L A. L. Stands for aluminum, Aluminum is over here in the third column. All the way over here. In this 13th column actually. So this is out next we have C S Gcse um here it is right here. It's in the first column it's pretty low down there. It's 1 32.91 for its atomic mass. Remember that could be in grams per mole atomic mass units. Or dalton's so far, it looks like it's the highest one. The only one higher than that would be F R. Notice that in the bottom rows here, most of them are whole numbers, these are super large mass elements that are pretty unstable. They typically don't have numerous isotopes as a result they have no decimal places. So next so so far C looks like it's our best choice if we look at D. We have Ally, which is up here, not hiring mass, not greater atomic mass. And then we have N. A. Which is right here. So it looks like C is our best choice. It has the greatest mass atomic mass from column one from the choices provided. So just remember we have our element symbols, We have our atomic masses, which normally are not whole numbers, and then we actually have whole numbers. Those represent our atomic numbers.

Which of the following choices has the greatest atomic mass?

• A. Element A (0.283 kg)
• B. Element B (3.20 x 10²⁴ amu)
• C. Element C (0.350 kg)
• D. Element D (4.14 x 10²⁶ Da)

Atomic Mass (Simplified) Concept 2

Now the atomic mass of an element can be calculated if you know the isotopic masses and percent abundances. Now isotopic masses are the masses for all the isotopes of a given element and percent abundance sometimes referred to as natural abundances. These are the percentage is available for each of the isotopes of a given element. Now sometimes referred to as your percent natural abundances. I know it's a little bit redundant but just remember you might see percent abundances, natural abundances or percent natural abundances. Now isotopic abundance also called your fractional abundance. This is your percent abundance of an isotope divided by 100. And remember when you divide a percentage by 100 you're changing it from its percentage form to its fractional or decimal form. Now all of this together gives us our isotope, our atomic mass formula. Now atomic mass formula we're gonna say equals the isotopic mass of isotope one times its isotopic abundance. Plus the isotopic mass of isotope two times its isotopic abundance. Now of course if you have more than two isotopes for a given element, this will just continue. You would keep adding would say plus isotope mass three times its isotopic abundance, plus isotope mass, four times its isotopic abundance. In this example, we're just showing that this particular element we're talking about has two isotopes involved with it and they both have their own masses. But again, this formula can be expanded to even more isotopes depending on the element elements such as magnesium have various isotopes. So their formulas would be a lot larger.

Atomic Mass (Simplified) Example 2

in the following example. Question, it says calculate the atomic mass of gallium if galleon has two naturally occurring isotopes with the following masses and natural abundances. So here we're dealing with gallium 69 71. Their atomic masses are written in terms of atomic mass units, and then here we have 60.11% and 39.89%. Those represent the percent abundance is now to find the atomic mass of our gallium element. Let's follow step one. Step one says, if you are given percent abundances, which we were, we're going to divide them by 100 in order to isolate our fractional abundances. So divide them both y 100. When we do that, we're gonna get our fractional abundances. So then we have these now as our fractional abundances step to plug your given variables into the atomic mass formula in order to isolate the missing variable. So this is just a simple plug and chug algebraic type of situation. Our atomic mass of our element equals the mass of the first isotope times. It's fractional abundance, plus the mass of our second isotope times. It fractional abundance. So when we do that, we're gonna get 69. am you. Since our isotopic masses have four decimal places, we could follow four decimal places here. But we have multiple choice options and we're gonna go with the best answer, which would be option A for this particular question. So using the atomic mass formula is pretty simple. All we have to do is round up all the variables that you're given and isolate the one that's missing. From there, you can find your final answer.

Only three isotopes of magnesium exist on earth. ²⁴Mg is the most common form at 78.70% natural abundance with a mass of 23.98504 amu, ²⁵Mg has a 10.13% natural abundance, while ²⁶Mg has a natural abundance of 11.17% and a mass of 25.98259 amu. What is the mass of the ²⁵Mg isotope?

• A. 24.76171 amu
• B. 24.99030 amu
• C. 25.00138 amu
• D. 25.38402 amu

Silver has an atomic mass of 107.868 amu. The Ag-109 isotope (108.905 amu) is 48.16%. What is the amu of the other isotope?

• A. 106.905 amu
• B. 106.908 amu
• C. 106.903 amu
• D. 106.911 amu