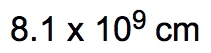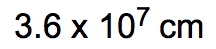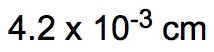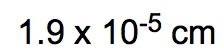Dimensional analysis is a systematic method used to convert one unit to another, ensuring accuracy in calculations by canceling out unwanted units. The process begins with a given amount and ends with the desired unknown amount, utilizing conversion factors to bridge the two. This technique is similar to metric prefix conversions, where units are aligned on opposite levels to facilitate cancellation.
For instance, if you start with a measurement of 32 inches and need to convert it to centimeters, you would use the conversion factor that states 1 inch equals 2.54 centimeters. By placing inches in the denominator, they cancel out, allowing you to multiply 32 by 2.54, resulting in 81.28 centimeters. However, it’s crucial to consider significant figures in your final answer. Since 32 has two significant figures, the result should be rounded to 81 centimeters.
In more complex conversions, such as converting 115 minutes to years, multiple conversion factors are employed. First, convert minutes to hours using the factor of 60 minutes per hour, then hours to days with the factor of 24 hours per day, and finally days to years using the factor of 365 days per year. This process involves canceling out units at each step, ultimately leading to the desired unit of years.
When calculating, multiply the conversion factors in the denominator (60, 24, and 365) to get a total of 525,600. Dividing 115 by this total gives approximately 2.19 × 10-4 years. The significant figures in the final answer are determined by the given amount, which in this case is 115, having three significant figures. Thus, the final answer is expressed as 2.19 × 10-4 years.
Overall, dimensional analysis is a powerful tool that relies on conversion factors to connect given amounts to desired units, emphasizing the importance of unit cancellation and significant figures in achieving accurate results.