Understanding significant figures is crucial for accurate data analysis and measurement interpretation. The concept of significant figures relates directly to the precision of a measurement; the more significant figures present, the more precise the measurement is. For instance, a measurement of 25.00 mL is more precise than 25 mL because the former includes a decimal point, indicating a higher level of detail. In this case, 25.00 mL has four significant figures, while 25 mL has only two.
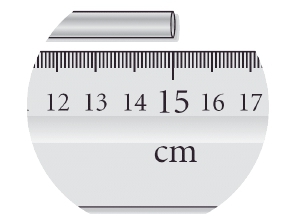
When recording measurements, it is essential to consider significant figures carefully. The rule of thumb is to include all known digits plus one estimated digit. This practice acknowledges the inherent uncertainty in measurements. For example, when using a measuring tape or a graduated cylinder, one should not simply read the measurement from the markings; instead, an additional decimal place should be estimated based on visual assessment, often referred to as the "eyeball test." This approach ensures that the recorded value reflects the appropriate number of significant figures, thereby enhancing the accuracy of the data.
In summary, significant figures play a vital role in conveying the precision of measurements. By adhering to the principles of significant figures, one can ensure that data analysis is both accurate and reliable, ultimately leading to more valid conclusions in scientific inquiry.