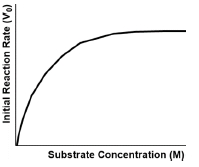
In enzyme-catalyzed reactions, understanding the initial velocity, denoted as \( v_0 \), is crucial for biochemists. The initial velocity represents the reaction rate at the very beginning when substrate concentration is at its highest and the reverse reaction, where products convert back to substrates, is negligible. As the reaction progresses, substrate concentration decreases because it is being converted into products, leading to a natural decline in reaction rate. This relationship highlights that higher substrate concentrations correlate with higher reaction rates, while lower concentrations result in slower rates.
As time passes, the accumulation of products increases the significance of the reverse reaction, complicating the measurement of the forward reaction rate. Therefore, the initial velocity provides the best approximation of the maximum velocity, \( v_{max} \), that an enzyme can achieve, although enzymes can only approach this maximum rather than attain it. This concept will be explored in greater detail in future discussions.
Graphical representations of these reactions illustrate the dynamics at play. For instance, a graph plotting product concentration against time shows a curve that eventually levels off, indicating that equilibrium has been reached when the rate of the forward reaction equals the rate of the reverse reaction. The slope of the tangent line at the beginning of this curve gives the initial reaction rate, calculated as the change in product concentration over the change in time.
Another graph, which plots reaction rate against time, demonstrates that the reaction rate decreases as time progresses. This decline reinforces the idea that the initial reaction rate, \( v_0 \), is the fastest rate observed early in the reaction. All enzyme kinetics calculations moving forward will assume that the measured reaction velocity is the initial velocity, facilitating comparisons across different enzyme-catalyzed reactions. Understanding these principles lays the groundwork for further exploration of enzyme kinetics and related concepts in subsequent lessons.