16. Angular Momentum
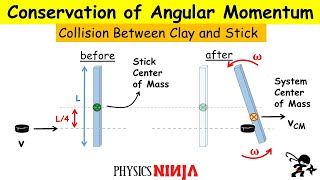
Conservation of Angular Momentum
Learn with other creators
Practice this topic
- Multiple Choice
Suppose a diver spins at 8 rad/s while falling with a moment of inertia about an axis through himself of 3 kg•m2. What moment of inertia would the diver need to have to spin at 4 rad/s?
BONUS:How could he accomplish this?
859views10rank1comments - Multiple Choice
Two astronauts, both 80 kg, are connected in space by a light cable. When they are 10 m apart, they spin about their center of mass with 6 rad/s. Calculate the new angular speed they'll have if they pull on the rope to reduce their distance to 5 m. You may treat them as point masses, and assume they continue to spin around their center of mass.
921views7rank - Textbook Question
The rotor (flywheel) of a toy gyroscope has mass 0.140 kg. Its moment of inertia about its axis is 1.20 × 10-4 kg m2. The mass of the frame is 0.0250 kg. The gyroscope is supported on a single pivot (Fig. E10.51) with its center of mass a horizontal distance of 4.00 cm from the pivot. The gyroscope is precessing in a horizontal plane at the rate of one revolution in 2.20 s. Find the upward force exerted by the pivot.
<Image>
1349views - Textbook Question
Under some circumstances, a star can collapse into an extremely dense object made mostly of neutrons and called a neutron star. The density of a neutron star is roughly times as great as that of ordinary solid matter. Suppose we represent the star as a uniform, solid, rigid sphere, both before and after the collapse. The star's initial radius was (comparable to our sun); its final radius is 16 km. If the original star rotated once in days, find the angular speed of the neutron star.
3152views1rank - Textbook Question
A thin uniform rod has a length of and is rotating in a circle on a frictionless table. The axis of rotation is perpendicular to the length of the rod at one end and is stationary. The rod has an angular velocity of and a moment of inertia about the axis of . A bug initially standing on the rod at the axis of rotation decides to crawl out to the other end of the rod. When the bug has reached the end of the rod and sits there, its tangential speed is . The bug can be treated as a point mass. What is the mass of the rod.
3097views1comments - Textbook Question
A large wooden turntable in the shape of a flat uniform disk has a radius of 2.00 m and a total mass of 120 kg. The turntable is initially rotating at 3.00 rad/s about a vertical axis through its center. Suddenly, a 70.0-kg parachutist makes a soft landing on the turntable at a point near the outer edge. Compute the kinetic energy of the system before and after the parachutist lands. Why are these kinetic energies not equal?
1828views - Multiple Choice
Under what condition is the angular momentum of an object conserved?
46views - Multiple Choice
In the context of conservation of angular momentum, consider the system shown in Figure 2, part e. For which of the following diagrams is the (angular momentum) of the system constant?
43views