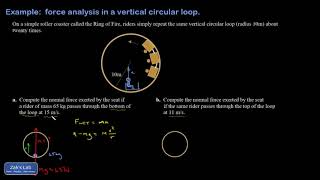
8. Centripetal Forces & Gravitation

The physics of circular motion sets an upper limit to the speed of human walking. (If you need to go faster, your gait changes from a walk to a run.) If you take a few steps and watch what's happening, you'll see that your body pivots in circular motion over your forward foot as you bring your rear foot forward for the next step. As you do so, the normal force of the ground on your foot decreases and your body tries to 'lift off' from the ground. a. A person's center of mass is very near the hips, at the top of the legs. Model a person as a particle of mass m at the top of a leg of length L. Find an expression for the person's maximum walking speed vₘₐₓ.

Suppose you swing a ball of mass m in a vertical circle on a string of length L. As you probably know from experience, there is a minimum angular velocity ωₘᵢₙ you must maintain if you want the ball to complete the full circle without the string going slack at the top. a. Find an expression for ωₘᵢₙ.

In an amusement park ride called The Roundup, passengers stand inside a 16-m-diameter rotating ring. After the ring has acquired sufficient speed, it tilts into a vertical plane, as shown in FIGURE P8.51. b. What is the longest rotation period of the wheel that will prevent the riders from falling off at the top?

A heavy ball with a weight of 100 N (m = 10.2 kg) is hung from the ceiling of a lecture hall on a 4.5-m-long rope. The ball is pulled to one side and released to swing as a pendulum, reaching a speed of 5.5 m/s as it passes through the lowest point. What is the tension in the rope at that point?

A 500 g ball moves in a vertical circle on a 102-cm-long string. If the speed at the top is 4.0 m/s, then the speed at the bottom will be 7.5 m/s. (You'll learn how to show this in Chapter 10.) (b) What is the tension in the string when the ball is at the top?

A 500 g ball moves in a vertical circle on a 102-cm-long string. If the speed at the top is 4.0 m/s, then the speed at the bottom will be 7.5 m/s. (You'll learn how to show this in Chapter 10.) (a) What is the gravitational force acting on the ball?

The normal force equals the magnitude of the gravitational force as a roller-coaster car crosses the top of a 40-m-diameter loop-the-loop. What is the car's speed at the top?

The weight of passengers on a roller coaster increases by 50% as the car goes through a dip with a 30 m radius of curvature. What is the car's speed at the bottom of the dip?

A car drives over the top of a hill that has a radius of 50 m. What maximum speed can the car have at the top without flying off the road?