Significant Figures: Precision in Measurements: Videos & Practice Problems

Significant figures are crucial in data analysis, indicating the precision of measurements. More significant figures imply greater precision; for instance, 25.00 mL (4 sig figs) is more precise than 25 (2 sig figs). When recording measurements, include all known digits plus an estimated decimal place to account for uncertainty. This practice ensures accurate representation of data, essential for scientific calculations and understanding concepts like activation energy and acid dissociation constants. Mastering significant figures enhances analytical skills and supports effective communication of scientific findings.

Significant Figures Precision Concept

Significant figures are crucial in data analysis and affect the precision of our answers. The concept of significant figures indicates that the more significant figures a measurement has, the more precise it is. For instance, a measurement of 25.00 mL is more precise than 25 mL because the former includes a decimal point, indicating a higher level of detail. In the case of 25.00 mL, the first non-zero digit is 2, and counting all the way to the end gives us four significant figures. Conversely, 25 mL, which lacks a decimal point, has only two significant figures.

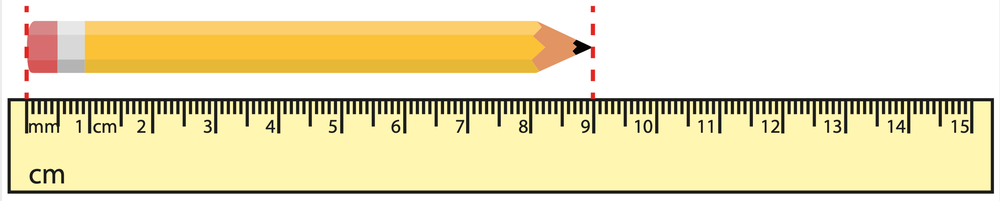
When recording measurements, it is essential to consider significant figures. The rule is to include all known digits plus one additional estimated digit. This practice is often referred to as the "eyeball test," which involves making an educated guess based on visual observation of measuring tools like beakers or measuring tapes. It is important to recognize that there is inherent uncertainty in these measurements, and simply relying on the visible markings is insufficient. Therefore, adding an extra decimal place helps ensure the correct number of significant figures is recorded, enhancing the accuracy of the measurement.

Significant Figures Precision Example

When determining the number of significant figures in a measurement, it is essential to understand how to accurately represent the precision of that measurement. In this example, the length of a square is measured at 3.2 centimeters, with hash marks indicating the values of 3.0, 3.1, and 3.2 centimeters. To express this measurement with the correct number of significant figures, one must consider the precision of the measurement tool used.

In this case, since the measurement is taken between the 3.2 and 3.3 centimeter marks, it is appropriate to include an additional decimal place to reflect the precision. Therefore, the measurement should be recorded as 3.20 centimeters. This notation indicates that the measurement is precise to the hundredths place, thus ensuring that the significant figures are accurately represented. Consequently, the best answer is 3.20 centimeters, which corresponds to option C.

Read the length of the pencil to the correct number of significant figures.

• A. 8.0 cm
• B. 8.000 cm
• C. 9 cm
• D. 9.0 cm
• E. 9.00 cm

Answer: (E)

What is the correct reading for the liquid in the burette provided below?

• A. 7 mL
• B. 7.0 mL
• C. 7.20 mL
• D. 7.00 mL
• E. 6.80 mL

Answer: (D)

Here’s what students ask on this topic:

What are significant figures and why are they important in scientific measurements?

Significant figures are the digits in a number that carry meaningful information about its precision. They include all known digits plus one estimated digit. In scientific measurements, significant figures are crucial because they indicate the precision of the measurement and help in accurately representing data. More significant figures mean higher precision. For example, 25.00 mL (4 sig figs) is more precise than 25 mL (2 sig figs). This precision is essential for scientific calculations, such as determining activation energy or acid dissociation constants, and ensures effective communication of scientific findings.

How do you determine the number of significant figures in a measurement?

To determine the number of significant figures in a measurement, follow these rules: 1) All non-zero digits are significant. 2) Any zeros between significant digits are also significant. 3) Leading zeros (zeros before the first non-zero digit) are not significant. 4) Trailing zeros in a decimal number are significant. For example, in 25.00 mL, the number has 4 significant figures because all digits, including the trailing zeros, are significant. In 0.025, only the 2 and 5 are significant, giving it 2 significant figures.

How do you handle significant figures in addition and subtraction?

When performing addition or subtraction, the result should be rounded to the least number of decimal places in any of the numbers being added or subtracted. For example, if you add 25.00 mL (2 decimal places) and 0.5 mL (1 decimal place), the result should be rounded to 1 decimal place, giving 25.5 mL. This ensures that the precision of the result is consistent with the precision of the least precise measurement.

How do you handle significant figures in multiplication and division?

In multiplication and division, the result should be rounded to the same number of significant figures as the measurement with the fewest significant figures. For example, if you multiply 25.00 mL (4 sig figs) by 2.0 (2 sig figs), the result should have 2 significant figures, giving 50 mL. This rule ensures that the precision of the result reflects the precision of the least precise measurement.

Why is it important to include an estimated decimal place in measurements?

Including an estimated decimal place in measurements is important because it accounts for the uncertainty inherent in any measurement. This practice ensures that all known digits are recorded, plus one additional digit that represents the best estimate. This additional decimal place enhances the precision of the measurement and provides a more accurate representation of the data, which is crucial for scientific calculations and analyses.