Metric Prefixes: Videos & Practice Problems

Metric prefixes are essential modifiers in chemistry, representing powers of ten. Common prefixes include tera (10¹²), giga (10⁹), mega (10⁶), kilo (10³), and milli (10^-3). These prefixes can be applied to base units like liters, seconds, moles, and amperes, facilitating conversions such as milliliters or nanoseconds. A mnemonic, "King Henry's Daughter Barbara Drinks Chocolate Milk Until 9 PM," aids in memorizing the order of prefixes. Understanding these prefixes is crucial for accurate measurements and calculations in scientific contexts.

Metric Prefixes

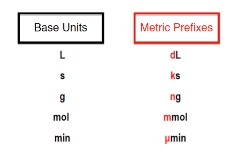
Understanding metric prefixes is essential for performing calculations in chemistry, as they serve as modifiers that represent multiples of ten. The metric prefix multipliers range from \(10^{12}\) to \(10^{-12}\), which is typically sufficient for introductory chemistry courses. For higher-level studies, prefixes such as \(10^{-15}\) and \(10^{15}\) may be encountered.

Here’s a breakdown of the common metric prefixes:

• Terra (T): \(10^{12}\)
• Giga (G): \(10^{9}\)
• Mega (M): \(10^{6}\)
• Kilo (k): \(10^{3}\) (as in kilometer)
• Hecto (h): \(10^{2}\)
• Deka (da): \(10^{1}\)
• Base Unit: (e.g., liters, seconds)
• Deci (d): \(10^{-1}\)
• Centi (c): \(10^{-2}\) (as in centimeter)
• Milli (m): \(10^{-3}\) (as in milliliters)
• Micro (µ): \(10^{-6}\)
• Nano (n): \(10^{-9}\)
• Pico (p): \(10^{-12}\)

To aid in memorization, a mnemonic device can be employed: "The great monarch, King Henry's daughter Barbara, drinks chocolate milk until 9 PM." Each initial corresponds to a metric prefix, helping to recall their order from \(10^{12}\) down to \(10^{-12}\).

As you study metric prefixes, remember to consult with your professor to confirm the specific range you need to master for your course. This foundational knowledge will be crucial as you apply these prefixes to base units in future calculations.

Metric Prefixes

Metric prefixes serve as essential labels that modify base units, allowing for a clearer understanding of measurements across various scientific disciplines. For instance, the base unit for volume is the liter, while time is measured in seconds, the amount of a substance in moles, and electrical current in amperes. These base units are integral to the International System of Units (SI).

By applying metric prefixes to these base units, we can create new units that represent different scales. For example, when we add the prefix "milli-" to liters, we obtain milliliters, which denotes one-thousandth of a liter. Similarly, "nano-" can be prefixed to seconds to form nanoseconds, representing one-billionth of a second. In the case of moles, the prefix "giga-" results in gigamoles, indicating one billion moles, while "kilo-" in front of amperes gives us kiloamperes, or one thousand amperes.

This process of prefixing is crucial for metric conversions, as it allows scientists and engineers to express quantities in a more manageable form. Understanding how to transition between different metric prefixes is a fundamental skill in scientific measurement and calculation.

Metric Prefixes Example 1

To convert units effectively, it's essential to understand metric prefixes and their relationships to base units. In this example, we will convert 694 kilograms to micrograms, following a systematic approach.

First, identify the metric prefix in the given value. Here, "kilo" is the prefix, which indicates a factor of \(10^3\). The base unit for kilograms is grams. Therefore, we start by converting kilograms to grams:

1. **Convert to Base Unit:**
\[ 694 \text{ kg} = 694 \times 10^3 \text{ g} \]

Next, to convert grams to micrograms, we need to recognize that "micro" represents a factor of \(10^{-6}\). To cancel out grams, we set up the conversion as follows:

2. **Convert to Desired Unit:**
\[ 694 \times 10^3 \text{ g} \times \frac{1 \text{ µg}}{10^{-6} \text{ g}} \]

By placing grams in the denominator, they will cancel out, allowing us to focus on the remaining units. Now, we can simplify the expression:

3. **Combine the Exponents:**
\[ 694 \times 10^3 \div 10^{-6} = 694 \times 10^{3 - (-6)} = 694 \times 10^{3 + 6} = 694 \times 10^9 \text{ µg} \]

4. **Final Calculation:**
To express this in scientific notation, we can rewrite 694 as \(6.94 \times 10^2\), leading to:

\[ 6.94 \times 10^2 \times 10^9 \text{ µg} = 6.94 \times 10^{11} \text{ µg} \]

Thus, the final result of converting 694 kilograms to micrograms is:

\[ 6.94 \times 10^{11} \text{ µg} \]

This process illustrates the importance of understanding metric prefixes and their conversions, allowing for accurate unit transformations in scientific calculations.

Which quantity in the following pair is smaller?

• A. 155 pm
• B. 7.8 x 10^–9 cm

Answer: (B)

Use the prefix multipliers to express each measurement without any exponents.
a) 32 x 10^-13 L
b) 7.3 x 10⁶ g 
c) 18.5 x 10¹¹ s

In this exercise, we focus on converting measurements expressed in scientific notation into standard notation using metric prefixes. This process involves understanding both scientific notation and the metric system's prefix multipliers.

To begin, consider the measurement of 32 times \(10^{-13}\) liters. The closest metric prefix to \(10^{-13}\) is pico, which corresponds to \(10^{-12}\). To convert liters to picoliters, we set up the conversion as follows:

\[32 \times 10^{-13} \, \text{liters} \times \frac{1 \, \text{picoliter}}{10^{-12} \, \text{liters}} = 3.2 \, \text{picoliters}\]

Here, the liters cancel out, and the calculation yields 3.2 picoliters, effectively removing the exponent.

Next, we examine 7.3 times \(10^{6}\) grams. The metric prefix for \(10^{6}\) is mega. To convert grams to megagrams, we perform the following conversion:

\[7.3 \times 10^{6} \, \text{grams} \times \frac{1 \, \text{megagram}}{10^{6} \, \text{grams}} = 7.3 \, \text{megagrams}\]

Again, the grams cancel out, and we arrive at 7.3 megagrams.

Finally, we consider 18.5 times \(10^{11}\) seconds. The closest metric prefix here is tera, which represents \(10^{12}\). To convert seconds to teraseconds, we set up the conversion as follows:

\[18.5 \times 10^{11} \, \text{seconds} \times \frac{1 \, \text{terasecond}}{10^{12} \, \text{seconds}} = 1.85 \, \text{teraseconds}\]

With seconds canceling out, we find the result to be 1.85 teraseconds.

In summary, this exercise illustrates how to transition from scientific notation to standard notation by utilizing metric prefixes, effectively simplifying the representation of measurements while eliminating exponents.

Use scientific notation to express each quantity with only the base unit. 
a) 83 µm
b) 193 kg
c) 2.7 mmol

In scientific notation, expressing quantities with only the base unit involves understanding metric prefixes and their corresponding values. Each metric prefix represents a specific power of ten that modifies the base unit. For example, the prefix "micro" corresponds to \(10^{-6}\), "kilo" corresponds to \(10^{3}\), and "milli" corresponds to \(10^{-3}\).

To convert from micrograms (or micrometers) to meters, we recognize that "micro" is the prefix. To eliminate this prefix, we place it in the denominator. Thus, for a quantity of 8.3 micrograms, the conversion to meters is calculated as follows:

\[8.3 \, \text{micrograms} \times \left( \frac{1 \, \text{gram}}{10^{-6} \, \text{grams}} \right) = 8.3 \times 10^{-5} \, \text{meters}\]

Next, converting kilograms to grams involves the prefix "kilo." Here, we again place the prefix in the denominator. For 193 kilograms, the conversion to grams is:

\[193 \, \text{kilograms} \times \left( \frac{10^{3} \, \text{grams}}{1 \, \text{kilogram}} \right) = 1.93 \times 10^{5} \, \text{grams}\]

Finally, when converting millimoles to moles, the prefix "milli" is used. To convert 2.7 millimoles to moles, we proceed similarly:

\[2.7 \, \text{millimoles} \times \left( \frac{1 \, \text{mole}}{10^{-3} \, \text{millimoles}} \right) = 2.7 \times 10^{-3} \, \text{moles}\]

In summary, converting from metric prefixes to base units requires recognizing the appropriate power of ten associated with each prefix and applying it correctly in calculations. This process not only simplifies the units but also allows for the expression of quantities in scientific notation.

If a room has a volume of 1.15 x 10⁸ cm³, what is the volume in km³?

• A. 1150 km³
• B. 115 km³
• C. 1.15 x 10^-7 km³
• D. 1.15 x 10⁵ km³

Answer: (C)

Here’s what students ask on this topic:

What are the common metric prefixes and their corresponding powers of ten?

Common metric prefixes and their corresponding powers of ten include:

• Tera (T): 10¹²
• Giga (G): 10⁹
• Mega (M): 10⁶
• Kilo (k): 10³
• Hecto (h): 10²
• Deka (da): 10¹
• Base unit: 10⁰
• Deci (d): 10^-1
• Centi (c): 10^-2
• Milli (m): 10^-3
• Micro (μ): 10^-6
• Nano (n): 10^-9
• Pico (p): 10^-12

These prefixes are used to modify base units like liters, seconds, moles, and amperes, making it easier to express very large or very small quantities.

How can I memorize the order of metric prefixes?

A helpful mnemonic to memorize the order of metric prefixes is: "King Henry's Daughter Barbara Drinks Chocolate Milk Until 9 PM." Each word's initial corresponds to a prefix:

• King (Kilo, 10³)
• Henry (Hecto, 10²)
• Daughter (Deka, 10¹)
• Barbara (Base unit, 10⁰)
• Drinks (Deci, 10^-1)
• Chocolate (Centi, 10^-2)
• Milk (Milli, 10^-3)
• Until (Micro, 10^-6)
• 9 (Nano, 10^-9)
• PM (Pico, 10^-12)

This mnemonic helps in recalling the order from larger to smaller prefixes.

How do metric prefixes facilitate conversions in scientific measurements?

Metric prefixes facilitate conversions by providing a standardized way to express large and small quantities. For example, instead of writing 0.000001 liters, you can write 1 microliter (μL). This simplifies calculations and communication in scientific contexts. By using prefixes like milli (10^-3), micro (10^-6), and kilo (10³), you can easily convert between units. For instance, 1 kilometer (km) is 1000 meters (m), and 1 milliliter (mL) is 0.001 liters (L). Understanding these prefixes is crucial for accurate measurements and conversions in chemistry, physics, and other sciences.

What are some examples of metric prefixes applied to base units?

Metric prefixes can be applied to various base units to express different magnitudes. Here are some examples:

• Volume: Milliliters (mL) - 10^-3 liters
• Time: Nanoseconds (ns) - 10^-9 seconds
• Amount of substance: Gigamoles (Gmol) - 10⁹ moles
• Electrical current: Kiloamperes (kA) - 10³ amperes

These prefixes help in expressing very large or very small quantities in a more manageable form, making calculations and communication more efficient in scientific work.

Why are metric prefixes important in scientific measurements?

Metric prefixes are important in scientific measurements because they provide a standardized way to express and convert large and small quantities. This standardization ensures consistency and accuracy in scientific communication and calculations. For example, using prefixes like kilo (10³), milli (10^-3), and micro (10^-6) allows scientists to easily convert between units and understand the scale of measurements. This is crucial in fields like chemistry, physics, and engineering, where precise measurements are essential for experiments, data analysis, and technological development.