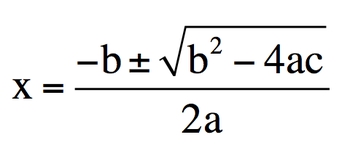So here we're dealing with the quadratic formula. We're going to say the quadratic formula is used for algebraic equations that contain a variable X raised to the second power. Now a customary expression is AX2 + b * X + C OK, so here A&B are just numerical values. OK, so they're actual numbers they're saying here. Oh, and same thing with C as well. X is our just missing variables.
We're going to see the quadratic formula which is shown here. It's X = − b ± b 2 − 4 A C 2 A . Here it says the quadratic formula is most commonly used for questions dealing with chemical equilibrium. So when we get to on the sections dealing with chemical equilibrium, we're going to use things that are called ice charts. And these ICE charts helped me to find equilibrium concentrations. So equilibrium amounts or concentrations. That's when we typically use these. Now you may use the quadratic formula before then within your labs, so it's so important to remember.
So we're going to say although the presence of the positive negative sign gives 2 possible values for X, only one of them will be significant and used as the answer. So again, because there's a plus or minus here, that means we have a possibility of two answers for our X when we do different types of questions, usually means that we have only one possibility when it comes to our final answer. Now knowing this, let's see if we can solve this question. Here it says using the quadratic formula, solve for X when given the following algebraic expression. So let me take myself out of the image guys, because we need room to do this.
So we're going to say here we have 4 X = 2 . 13 × 10 − 4 − 2 . 13 × 10 − 4 × 10 − 4 / X . Again, we want our expression to look something like this, and we want at least to have an X that is squared to be able to do the quadratic. Formula. Here we don't have that, and we have this number over X. So what we're going to do here is we're going to multiply both sides by X, and when we do that, we're going to get 4 X 2 = − 2 . 13 × 10 − 4 X . This X will cancel out with this X. So we're going to get 1.7 plus 1 . 75 × 10 − 5 . All right.
Now we're going to say that this X variable has the larger power, so it's our lead term. That means that everything has to meet be moved over to its side. So we're going to add 2 . 13 × 10 − 4 X to both sides, and then we're going to subtract 1 . 75 × 10 − 5 from both sides. So here what we're going to get at the end for our expression is 4 X 2 + 2 . 13 × 10 − 4 X − 1 . 75 × 10 − 5 . So this represents my a, my B and my C So my quadratic formula is. Remember, negative B, plus or minus go up up, so you can see it ± b 2 − 4 A C b 2 − 4 C / 2 A .
All right, so here the sign of B is positive, so I throw it in. It's going to become negative now ± b 2 − 4 A C . The value in front of A is a four and then C The value is this. Do not forget the negative sign. OK, so if there was a negative sign here for B, let's say that this was negative, then this would have been positive, would have been the opposite, and then we would have had to put the negative there as well. OK, so don't forget the signs get introduced as well, divided by 2 * 4. Alright, so oops, so now we're going to say that I'm going to take the square root of everything in here.
OK, So what I'm going to do first I'm going to figure out what everything is in there. Now if you do it correctly in your calculator, you should get 2.80 × 10 − 4 / 8 . Then realize you're going to get 2X variables, because remember it's plus or minus, so X here equals − 2.13 × 10 − 4 + 0.16735 / 8 , so that'll give me 0.002065 for X. Then remember we can also have X equals − 2.13 × 10 − 4 − 0.16735 / 8 and in this case X equals negative .002119.
So these are my 2 answers that X could be. Again, when we finally use this within our lectures, we're going to be using it for usually equilibrium questions. So chemical equilibrium questions, and only one of these answers will be the vital answer, and usually it's the positive answer is the one that we use. We discard the -1, but we'll talk about that later on when we're dealing with chemical equilibrium, ice charts and all that stuff. But for now, just remember what the quadratic formula is, what makes it up, and how the expression needs to be. Needs to take on the form of X2 plus BX plus C to give us the variables that we need in order to solve for X. We'll get 2 answers, and usually only one of them is a viable answer. The other one will be discarded. We'll talk about the conditions and reasons for discarding which one later on.