Density of Geometric Objects: Videos & Practice Problems

Understanding the relationship between mass, volume, and density is crucial in chemistry. Density is defined as mass divided by volume. This concept extends to geometric shapes such as spheres, cubes, and cylinders, each with its own volume formula. The volume of a sphere is calculated using:

$V=\frac{4\pi r^3}{3}$

where r is the radius. For a cube, the volume is:

$a^3$

with a representing the edge length. A cylinder's volume is found with:

$V=\pi r^{2}h$

incorporating both the radius and the height. These formulas allow us to solve density-related problems by connecting the mass of an object to its geometric volume. Generally, these volume equations are provided by instructors or found on formula sheets, so memorization is not required.

Density of Geometric Objects

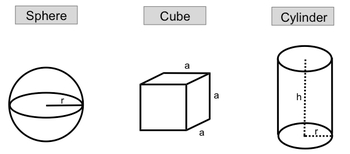
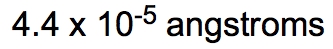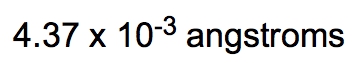Density is defined as the mass of an object divided by its volume, expressed mathematically as:

D = \frac{m}{V}

where D is density, m is mass, and V is volume. This concept can be applied to various geometric shapes, each with its own volume formula.

For a sphere, the volume can be calculated using the formula:

V = \frac{4}{3} \pi r^3

Here, r represents the radius, which is the distance from the center of the sphere to its surface. Understanding this formula allows you to determine the volume of a sphere when the radius is known.

In the case of a cube, where all sides are equal in length, the volume is given by:

V = a^3

In this formula, a denotes the length of one edge of the cube. This straightforward relationship highlights how the volume increases with the cube of the edge length.

For a cylinder, the volume is determined by both the radius and the height, expressed as:

V = \pi r^2 h

In this equation, r is the radius of the base of the cylinder, and h is the height. This formula illustrates how the volume of a cylinder is influenced by both its base area and its height.

By applying these volume formulas, you can solve density-related problems for spheres, cubes, and cylinders, allowing for a deeper understanding of how mass and volume interact in geometric contexts.

Density of Geometric Objects Example

To determine the mass of a cube of silver measuring 0.56 meters on each side, we start by recognizing the density of silver, which is 10.5 grams per cubic centimeter. The first step is to convert the dimensions of the cube from meters to centimeters, as the density is given in grams per cubic centimeter. Since 1 meter equals 100 centimeters, the side length of the cube in centimeters is:

0.56 \, \text{m} \times 100 \, \text{cm/m} = 56 \, \text{cm}

Next, we calculate the volume of the cube using the formula for volume:

V = \text{length}^3 = (56 \, \text{cm})^3 = 175616 \, \text{cm}^3

Now that we have the volume, we can use the density to find the mass. The formula relating mass, density, and volume is:

m = \text{density} \times \text{volume}

Substituting the known values:

m = 10.5 \, \text{g/cm}^3 \times 175616 \, \text{cm}^3 = 1843.968 \, \text{g}

To convert grams to kilograms, we use the conversion factor where 1 kilogram equals 1000 grams:

m = \frac{1843.968 \, \text{g}}{1000 \, \text{g/kg}} = 1.843968 \, \text{kg}

Considering significant figures, the original measurement of 0.56 meters has 2 significant figures, while the density of silver has 3 significant figures. Therefore, we round our final answer to 2 significant figures, resulting in:

m \approx 1.8 \times 10^3 \, \text{kg} \text{ or } 1800 \, \text{kg}

This example illustrates the importance of dimensional analysis and unit conversion in solving problems involving density and volume. By carefully managing units and significant figures, we can arrive at a precise and accurate answer.

A copper wire (density = 8.96 g/cm³) has a diameter of 0.32 mm. If a sample of this copper wire has a mass of 21.7 g, how long is the wire?

• A.
• B.
• C.
• D.
• E.

Answer: (B)

If the density of a certain spherical atomic nucleus is 1.0 x 10¹⁴ g/cm³ and its mass is 3.5 x 10^-23 g, what is the radius in angstroms? (Å= 10⁻¹⁰ m)

• A.
• B.
• C.
• D.
• E.

Answer: (C)

Here’s what students ask on this topic:

How do you find the density of a cylinder?

To find the density of a cylinder, you need to know two things: the mass of the cylinder and its volume. Density is defined as mass per unit volume. The formula for density (ρ) is:

$\rho =\frac{\mathrm{mass}}{\mathrm{volume}}$

First, measure the mass of the cylinder using a scale, ensuring you have the mass in kilograms (kg) or grams (g).

Next, calculate the volume of the cylinder. The volume of a cylinder is found using the formula:

$V=\Pi r^{2}h$

where:

• $\Pi$ (pi) is approximately 3.14159
• $r$ is the radius of the base of the cylinder
• $h$ is the height of the cylinder

Make sure to use consistent units when calculating the volume (e.g., if you're using centimeters for the radius and height, the volume will be in cubic centimeters).

Once you have both the mass and the volume, divide the mass by the volume to get the density. Ensure that your final density units are consistent (e.g., grams per cubic centimeter or kilograms per cubic meter).

How do you find the density of a cube?

To find the density of a cube, you'll need to know two key pieces of information: the mass of the cube and its volume. The formula for density (ρ) is:

$\rho =\frac{\mathrm{mass}}{\mathrm{volume}}$

First, measure the mass of the cube using a balance or scale, ensuring you have the mass in grams (g) or kilograms (kg). To calculate the volume of the cube, measure the length of one of its edges, since all edges of a cube are equal. Let's call this measurement 'a'. The volume (V) is then found by cubing this edge length:

$V=a^3$

Once you have both the mass (m) and the volume (V), plug these values into the density formula:

$\rho =\frac{m}{V}$

Make sure your units are consistent (e.g. if mass is in grams, volume should be in cubic centimeters for the density to be in grams per cubic centimeter). Calculate the quotient to find the density, which will give you an understanding of how much mass is contained in a certain volume of the cube.

How do you find the density of a sphere?

To find the density of a sphere, you need to know two key pieces of information: the mass of the sphere and its volume. The formula for density (ρ) is:

$\rho =\frac{\mathrm{mass}}{\mathrm{volume}}$

First, measure the mass of the sphere using a scale. This should be straightforward and is given in units of mass such as grams (g) or kilograms (kg).

Next, calculate the volume of the sphere. The volume (V) of a sphere is calculated using the formula:

$V=\frac{4}{3}\Pi r^3$

Here, 'r' is the radius of the sphere. Measure the diameter of the sphere and divide by two to get the radius. Make sure to use the same unit of measurement for the radius as you will for the volume.

Once you have the volume, divide the mass of the sphere by this volume to get the density. Ensure that your units are consistent when performing these calculations (e.g. if mass is in grams, volume should be in cubic centimeters for the density in g/cm³).

Remember, the density will be a measure of how much mass is contained in a given volume of the sphere.