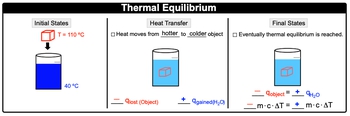
Thermal Equilibrium

thermal equilibrium is when two substances in physical contact with one another are at the same temperature. Now with the same temperature, these two substances would no longer exchange thermal energy by way of the first law of thermodynamics. So we take a look here, let's say we have this heated metal cube here and it's initially at a temperature of 110°C, and we're gonna place it into water at 40°C. Remember heat transfers when it comes to heat, it always moves from hotter to colder object. So the cube will be losing some heat. So some of the heat from the cube will be lost and it's gonna go into the water. So we say here that the cube is losing heat. So would have a negative cube and the water is absorbing that heat. So it'll be a positive Q. For the water. Eventually though the Q will no longer be able to release any more heat because it will get to the same temperature as the water. So it's at that moment we've reached thermal equilibrium. Now at thermal equilibrium, we can say here that they're both gonna have the same heat. So the negative Q. Of the object, hotter object will be equal to the positive Q of water in this case. And if their cues or heats are equal to one another, then there M. Cat formulas are equal to each other because remember Q equals M. Cat. So negative M. Cat equals positive M. Cat. Now under ideal thermal equilibrium, he transfers only occur between the solvent and the immersed heated object. If the situation is not ideal, then then we can say that that additional he could be absorbed by the calorie meter. So the calorie meter or the container in this case same thing would absorb some of that heat of the object. So here this equation would expand out under non ideal conditions to be negative Q. Of the object equals positive Q. Of the water plus Q. Of the container, also known as the calorie meter. So just remember if your professor is mentioning that this is a pure thermal equilibrium type of question, then you could just say Q. Negative Q. Hotter object equals positive Q. Of colder object, but if the calorie meter is involved, you have to take into account that it too would absorb some of this heat that's coming off of the hotter object.

here in this example question. It says if 50 g block of lead at 250 degrees Celsius, it submerged in the solution and 90 degrees Celsius, the final temperature of the solution will be. So let's just think about it. We have a container. We have, ah, hot piece of lead here, being submerged in some colder water, so try to use everyday real experiences here. What happens? I take a hot pan and I dunk it into the sink filled with water. We'll hear the pants sizzle. That's because the pan is releasing its extra heat into the water. The water is becoming Vape arised. Remember thermal equilibrium. They're both going to reach a temperature. That's the same for both of them. The temperature that they reach should be a temperature somewhere between 150 degrees Celsius and 90 degrees Celsius, because we'd expect the hotter object to release enough heat so that it and the the solvent that it's in can reach the same temperature. So about hotter object cools down some. The colder object warms up some. Their new final temperature will exist somewhere between their two initial temperatures, so we expect that the temperature of the solution to be greater than 90 degrees Celsius it will be a number between 1 50 90 degrees Celsius.