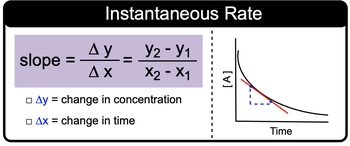
The instantaneous rate of a reaction refers to the rate at a specific moment in time, which can be determined by calculating the slope of the tangent line to the curve at that point on a graph. This method allows us to analyze the relationship between the concentration of reactants and time. When given a plot with coordinates (x, y), the slope can be calculated using the formula:
Slope = \(\frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1}\)
In this context, \(\Delta y\) represents the change in concentration of the reactants, while \(\Delta x\) signifies the change in time. As the reaction progresses, the overall rate of reaction typically decreases due to the diminishing amount of reactants. However, the instantaneous rate at any given moment can remain constant, depending on the specific conditions of the reaction.
To effectively calculate the instantaneous rate, one must identify two points on the curve that correspond to the tangent line. By applying the slope formula, one can derive the instantaneous rate of the reaction at that particular point. This approach is essential for understanding the dynamics of chemical reactions and for solving related problems in kinetics.