Heating and cooling curves are essential tools for understanding the heat absorbed or released by a substance during phase changes. The variable used to represent heat is q. In a heating curve, a substance absorbs heat, indicating an endothermic process where q is positive. Conversely, in a cooling curve, the substance releases heat, signifying an exothermic process where q is negative.
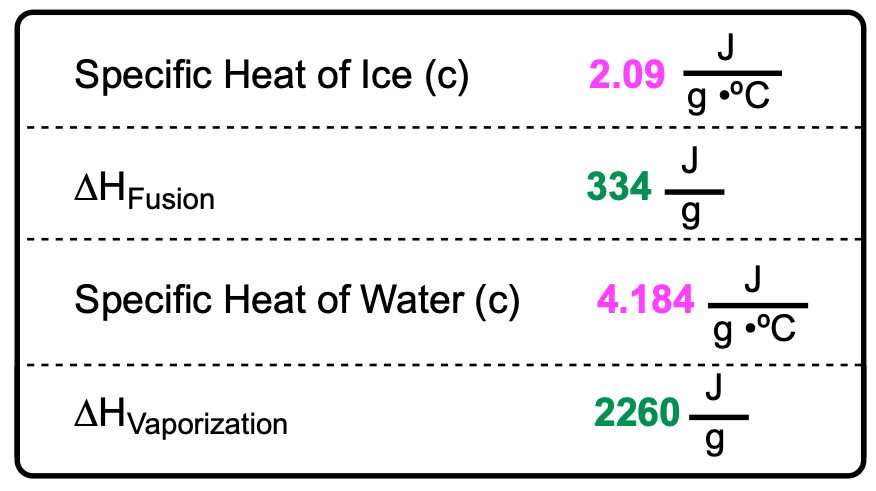
Taking water as an example, it can exist in three phases: solid, liquid, and gas. At 0 degrees Celsius, ice can melt into liquid water. During this phase change, the temperature remains constant, resulting in a plateau on the heating curve. This plateau occurs because the absorbed heat is used to break the bonds between molecules, facilitating the transition from solid to liquid, a process known as melting or fusion.
Once all the ice has melted, the temperature of the liquid water begins to rise. At 100 degrees Celsius, the water can undergo another phase change, transitioning from liquid to gas through vaporization. If additional heat is supplied, the temperature of the gaseous water continues to increase.
In contrast, the cooling curve for water starts with water vapor at a temperature above 100 degrees Celsius. As it cools, it releases energy until it reaches 100 degrees Celsius, where it undergoes condensation, transitioning from gas to liquid. This phase change also results in a plateau, as the temperature remains constant while the gas condenses into a liquid. The liquid then continues to release heat until it reaches 0 degrees Celsius, where it freezes into solid ice, marking another plateau in the cooling curve.
These heating and cooling curves can be viewed as mirror images of each other. Both vaporization and condensation occur at 100 degrees Celsius, while melting and freezing occur at 0 degrees Celsius. The plateaus in the curves indicate the temperature remains constant during phase changes, allowing the substance to fully convert into a new phase before continuing to change temperature. Understanding these concepts is crucial for further calculations related to heat transfer and phase changes.