1. Intro to General Chemistry
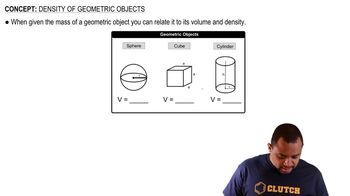
Density of Geometric Objects
Problem 115b
Textbook Question
Textbook QuestionImagine that you place a cork measuring 1.30 cm * 5.50 cm * 3.00 cm in water and that on top of the cork you place a small cube of lead measuring 1.15 cm on each edge. The density of cork is 0.235 g/cm3, and the density of lead is 11.35 g/cm3. Will the combination of cork plus lead float or sink?
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
1402
views
Was this helpful?
Related Videos
Related Practice
Showing 1 of 10 videos