1. Intro to General Chemistry
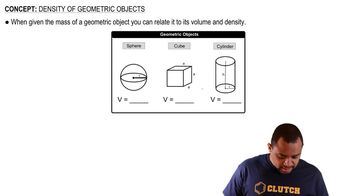
Density of Geometric Objects
Problem 115a
Textbook Question
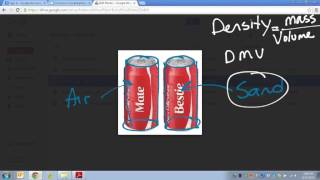
Textbook QuestionA thief uses a can of sand to replace a solid gold cylinder that sits on a weight-sensitive, alarmed pedestal. The can of sand and the gold cylinder have exactly the same dimensions (length = 22 and radius = 3.8 cm). a. Calculate the mass of each cylinder (ignore the mass of the can itself). (density of gold = 19.3 g>cm3, density of sand = 3.00 g>cm3) b. Does the thief set off the alarm? Explain.
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
563
views
Was this helpful?
Related Videos
Related Practice
Showing 1 of 10 videos