1. Intro to General Chemistry
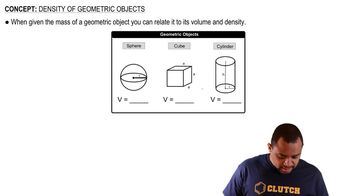
Density of Geometric Objects

Get help from an AI Tutor
Ask a question to get started.
Problem 110
Textbook Question
Textbook QuestionLignum vitae is a hard, durable, and extremely dense wood used to make ship bearings. A sphere of this wood with a diameter of 7.60 cm has a mass of 313 g. (a) What is the density of the lignum vitae sphere? (b) Will the sphere float or sink in water? (c) Will the sphere float or sink in chloroform? (The density of chloroform is 1.48 g/mL.)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
612
views
Was this helpful?
Related Videos
Related Practice
Showing 1 of 10 videos