Significant figures are crucial in data analysis and affect the precision of our answers. The concept of significant figures indicates that the more significant figures a measurement has, the more precise it is. For instance, a measurement of 25.00 mL is more precise than 25 mL because the former includes a decimal point, indicating a higher level of detail. In the case of 25.00 mL, the first non-zero digit is 2, and counting all the way to the end gives us four significant figures. Conversely, 25 mL, which lacks a decimal point, has only two significant figures.
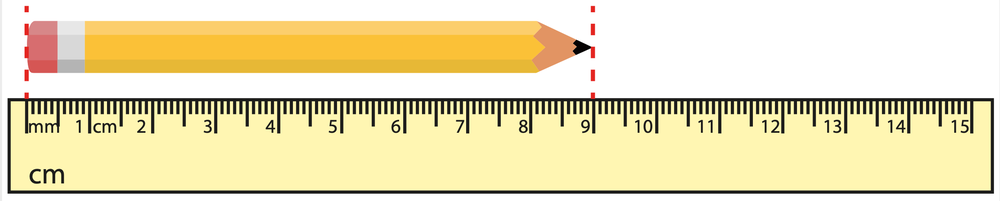
When recording measurements, it is essential to consider significant figures. The rule is to include all known digits plus one additional estimated digit. This practice is often referred to as the "eyeball test," which involves making an educated guess based on visual observation of measuring tools like beakers or measuring tapes. It is important to recognize that there is inherent uncertainty in these measurements, and simply relying on the visible markings is insufficient. Therefore, adding an extra decimal place helps ensure the correct number of significant figures is recorded, enhancing the accuracy of the measurement.