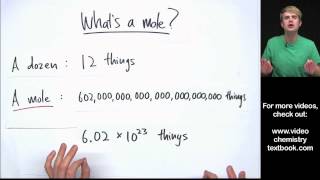2. Atoms & Elements
Mole Concept
Problem 113b
Textbook Question
Textbook QuestionA pure copper sphere has a radius of 0.935 in. How many copper atoms does it contain? [The volume of a sphere is (4>3)pr3 and the density of copper is 8.96 g/cm3.]
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
1509
views
Was this helpful?
Related Videos
Related Practice
Showing 1 of 15 videos