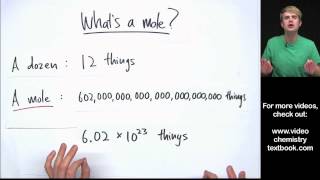2. Atoms & Elements
Mole Concept
Problem 118
Textbook Question
Textbook QuestionCommon brass is a copper and zinc alloy containing 37.0% zinc by mass and having a density of 8.48 g/cm3. A fitting composed of common brass has a total volume of 112.5 cm3. How many atoms (copper and zinc) does the fitting contain?
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
1505
views
1
rank
Was this helpful?
Related Videos
Related Practice
Showing 1 of 15 videos