Table of contents
- 1. Intro to General Chemistry3h 29m
- Physical & Chemical Changes19m
- Chemical Properties7m
- Physical Properties5m
- Intensive vs. Extensive Properties13m
- Temperature12m
- Scientific Notation13m
- SI Units7m
- Metric Prefixes24m
- Significant Figures9m
- Significant Figures: Precision in Measurements8m
- Significant Figures: In Calculations14m
- Conversion Factors16m
- Dimensional Analysis17m
- Density12m
- Density of Geometric Objects19m
- Density of Non-Geometric Objects7m
- 2. Atoms & Elements4h 16m
- The Atom9m
- Subatomic Particles15m
- Isotopes17m
- Ions27m
- Atomic Mass28m
- Periodic Table: Classifications11m
- Periodic Table: Group Names8m
- Periodic Table: Representative Elements & Transition Metals7m
- Periodic Table: Element Symbols6m
- Periodic Table: Elemental Forms6m
- Periodic Table: Phases8m
- Periodic Table: Charges20m
- Calculating Molar Mass10m
- Mole Concept30m
- Law of Conservation of Mass5m
- Law of Definite Proportions10m
- Atomic Theory9m
- Law of Multiple Proportions3m
- Millikan Oil Drop Experiment7m
- Rutherford Gold Foil Experiment10m
- 3. Chemical Reactions4h 10m
- Empirical Formula18m
- Molecular Formula20m
- Combustion Analysis38m
- Combustion Apparatus15m
- Polyatomic Ions24m
- Naming Ionic Compounds11m
- Writing Ionic Compounds7m
- Naming Ionic Hydrates6m
- Naming Acids18m
- Naming Molecular Compounds6m
- Balancing Chemical Equations13m
- Stoichiometry16m
- Limiting Reagent17m
- Percent Yield19m
- Mass Percent4m
- Functional Groups in Chemistry11m
- 4. BONUS: Lab Techniques and Procedures1h 36m
- 5. BONUS: Mathematical Operations and Functions48m
- 6. Chemical Quantities & Aqueous Reactions3h 53m
- Solutions6m
- Molarity18m
- Osmolarity15m
- Dilutions15m
- Solubility Rules15m
- Electrolytes18m
- Molecular Equations18m
- Gas Evolution Equations13m
- Solution Stoichiometry14m
- Complete Ionic Equations18m
- Calculate Oxidation Numbers15m
- Redox Reactions17m
- Balancing Redox Reactions: Acidic Solutions17m
- Balancing Redox Reactions: Basic Solutions17m
- Activity Series10m
- 7. Gases3h 50m
- Pressure Units6m
- The Ideal Gas Law18m
- The Ideal Gas Law Derivations13m
- The Ideal Gas Law Applications6m
- Chemistry Gas Laws13m
- Chemistry Gas Laws: Combined Gas Law12m
- Mole Fraction of Gases6m
- Partial Pressure19m
- The Ideal Gas Law: Molar Mass13m
- The Ideal Gas Law: Density14m
- Gas Stoichiometry18m
- Standard Temperature and Pressure14m
- Effusion14m
- Root Mean Square Speed9m
- Kinetic Energy of Gases10m
- Maxwell-Boltzmann Distribution8m
- Velocity Distributions4m
- Kinetic Molecular Theory14m
- Van der Waals Equation9m
- 8. Thermochemistry2h 37m
- Nature of Energy6m
- Kinetic & Potential Energy7m
- First Law of Thermodynamics7m
- Internal Energy8m
- Endothermic & Exothermic Reactions7m
- Heat Capacity19m
- Constant-Pressure Calorimetry24m
- Constant-Volume Calorimetry10m
- Thermal Equilibrium8m
- Thermochemical Equations12m
- Formation Equations9m
- Enthalpy of Formation12m
- Hess's Law23m
- 9. Quantum Mechanics2h 58m
- Wavelength and Frequency6m
- Speed of Light8m
- The Energy of Light13m
- Electromagnetic Spectrum10m
- Photoelectric Effect17m
- De Broglie Wavelength9m
- Heisenberg Uncertainty Principle17m
- Bohr Model14m
- Emission Spectrum5m
- Bohr Equation13m
- Introduction to Quantum Mechanics5m
- Quantum Numbers: Principal Quantum Number5m
- Quantum Numbers: Angular Momentum Quantum Number10m
- Quantum Numbers: Magnetic Quantum Number11m
- Quantum Numbers: Spin Quantum Number9m
- Quantum Numbers: Number of Electrons11m
- Quantum Numbers: Nodes6m
- 10. Periodic Properties of the Elements3h 9m
- The Electron Configuration22m
- The Electron Configuration: Condensed4m
- The Electron Configurations: Exceptions13m
- The Electron Configuration: Ions12m
- Paramagnetism and Diamagnetism8m
- The Electron Configuration: Quantum Numbers16m
- Valence Electrons of Elements12m
- Periodic Trend: Metallic Character3m
- Periodic Trend: Atomic Radius8m
- Periodic Trend: Ionic Radius13m
- Periodic Trend: Ionization Energy12m
- Periodic Trend: Successive Ionization Energies11m
- Periodic Trend: Electron Affinity10m
- Periodic Trend: Electronegativity5m
- Periodic Trend: Effective Nuclear Charge21m
- Periodic Trend: Cumulative12m
- 11. Bonding & Molecular Structure3h 29m
- Lewis Dot Symbols10m
- Chemical Bonds13m
- Dipole Moment11m
- Octet Rule10m
- Formal Charge9m
- Lewis Dot Structures: Neutral Compounds20m
- Lewis Dot Structures: Sigma & Pi Bonds14m
- Lewis Dot Structures: Ions15m
- Lewis Dot Structures: Exceptions14m
- Lewis Dot Structures: Acids15m
- Resonance Structures21m
- Average Bond Order4m
- Bond Energy15m
- Coulomb's Law6m
- Lattice Energy12m
- Born Haber Cycle14m
- 12. Molecular Shapes & Valence Bond Theory1h 58m
- 13. Liquids, Solids & Intermolecular Forces2h 23m
- Molecular Polarity10m
- Intermolecular Forces20m
- Intermolecular Forces and Physical Properties11m
- Clausius-Clapeyron Equation18m
- Phase Diagrams13m
- Heating and Cooling Curves27m
- Atomic, Ionic, and Molecular Solids11m
- Crystalline Solids4m
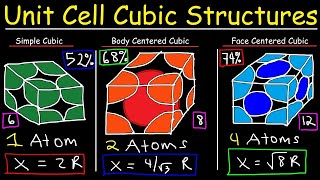
- Simple Cubic Unit Cell7m
- Body Centered Cubic Unit Cell12m
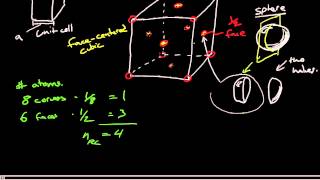
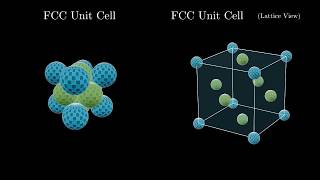
- Face Centered Cubic Unit Cell6m
- 14. Solutions3h 1m
- Solutions: Solubility and Intermolecular Forces17m
- Molality15m
- Parts per Million (ppm)13m
- Mole Fraction of Solutions8m
- Solutions: Mass Percent12m
- Types of Aqueous Solutions8m
- Intro to Henry's Law4m
- Henry's Law Calculations12m
- The Colligative Properties14m
- Boiling Point Elevation16m
- Freezing Point Depression10m
- Osmosis19m
- Osmotic Pressure10m
- Vapor Pressure Lowering (Raoult's Law)16m
- 15. Chemical Kinetics2h 53m
- 16. Chemical Equilibrium2h 29m
- 17. Acid and Base Equilibrium5h 2m
- Acids Introduction9m
- Bases Introduction7m
- Binary Acids15m
- Oxyacids10m
- Bases14m
- Amphoteric Species5m
- Arrhenius Acids and Bases5m
- Bronsted-Lowry Acids and Bases21m
- Lewis Acids and Bases12m
- The pH Scale16m
- Auto-Ionization9m
- Ka and Kb16m
- pH of Strong Acids and Bases9m
- Ionic Salts17m
- pH of Weak Acids31m
- pH of Weak Bases32m
- Diprotic Acids and Bases8m
- Diprotic Acids and Bases Calculations30m
- Triprotic Acids and Bases9m
- Triprotic Acids and Bases Calculations17m
- 18. Aqueous Equilibrium4h 47m
- Intro to Buffers20m
- Henderson-Hasselbalch Equation19m
- Intro to Acid-Base Titration Curves13m
- Strong Titrate-Strong Titrant Curves9m
- Weak Titrate-Strong Titrant Curves15m
- Acid-Base Indicators8m
- Titrations: Weak Acid-Strong Base38m
- Titrations: Weak Base-Strong Acid41m
- Titrations: Strong Acid-Strong Base11m
- Titrations: Diprotic & Polyprotic Buffers32m
- Solubility Product Constant: Ksp17m
- Ksp: Common Ion Effect18m
- Precipitation: Ksp vs Q12m
- Selective Precipitation9m
- Complex Ions: Formation Constant18m
- 19. Chemical Thermodynamics1h 50m
- 20. Electrochemistry2h 42m
- 21. Nuclear Chemistry2h 37m
- Intro to Radioactivity10m
- Alpha Decay9m
- Beta Decay7m
- Gamma Emission7m
- Electron Capture & Positron Emission9m
- Neutron to Proton Ratio7m
- Band of Stability: Alpha Decay & Nuclear Fission10m
- Band of Stability: Beta Decay3m
- Band of Stability: Electron Capture & Positron Emission4m
- Band of Stability: Overview14m
- Measuring Radioactivity7m
- Rate of Radioactive Decay12m
- Radioactive Half-Life16m
- Mass Defect19m
- Nuclear Binding Energy14m
- 22. Organic Chemistry5h 7m
- Introduction to Organic Chemistry8m
- Structural Formula8m
- Condensed Formula10m
- Skeletal Formula6m
- Spatial Orientation of Bonds3m
- Intro to Hydrocarbons16m
- Isomers11m
- Chirality15m
- Functional Groups in Chemistry11m
- Naming Alkanes4m
- The Alkyl Groups9m
- Naming Alkanes with Substituents13m
- Naming Cyclic Alkanes6m
- Naming Other Substituents8m
- Naming Alcohols11m
- Naming Alkenes11m
- Naming Alkynes9m
- Naming Ketones5m
- Naming Aldehydes5m
- Naming Carboxylic Acids4m
- Naming Esters8m
- Naming Ethers5m
- Naming Amines5m
- Naming Benzene7m
- Alkane Reactions7m
- Intro to Addition Reactions4m
- Halogenation Reactions4m
- Hydrogenation Reactions3m
- Hydrohalogenation Reactions7m
- Alcohol Reactions: Substitution Reactions4m
- Alcohol Reactions: Dehydration Reactions9m
- Intro to Redox Reactions8m
- Alcohol Reactions: Oxidation Reactions7m
- Aldehydes and Ketones Reactions6m
- Ester Reactions: Esterification4m
- Ester Reactions: Saponification3m
- Carboxylic Acid Reactions4m
- Amine Reactions3m
- Amide Formation4m
- Benzene Reactions10m
- 23. Chemistry of the Nonmetals2h 39m
- Main Group Elements: Bonding Types4m
- Main Group Elements: Boiling & Melting Points7m
- Main Group Elements: Density11m
- Main Group Elements: Periodic Trends7m
- The Electron Configuration Review16m
- Periodic Table Charges Review20m
- Hydrogen Isotopes4m
- Hydrogen Compounds11m
- Production of Hydrogen8m
- Group 1A and 2A Reactions7m
- Boron Family Reactions7m
- Boron Family: Borane7m
- Borane Reactions7m
- Nitrogen Family Reactions12m
- Oxides, Peroxides, and Superoxides12m
- Oxide Reactions4m
- Peroxide and Superoxide Reactions6m
- Noble Gas Compounds3m
- 24. Transition Metals and Coordination Compounds3h 16m
- Atomic Radius & Density of Transition Metals11m
- Electron Configurations of Transition Metals7m
- Electron Configurations of Transition Metals: Exceptions11m
- Paramagnetism and Diamagnetism10m
- Ligands10m
- Complex Ions5m
- Coordination Complexes7m
- Classification of Ligands11m
- Coordination Numbers & Geometry9m
- Naming Coordination Compounds22m
- Writing Formulas of Coordination Compounds8m
- Isomerism in Coordination Complexes15m
- Orientations of D Orbitals4m
- Intro to Crystal Field Theory10m
- Crystal Field Theory: Octahedral Complexes5m
- Crystal Field Theory: Tetrahedral Complexes4m
- Crystal Field Theory: Square Planar Complexes4m
- Crystal Field Theory Summary8m
- Magnetic Properties of Complex Ions9m
- Strong-Field vs Weak-Field Ligands6m
- Magnetic Properties of Complex Ions: Octahedral Complexes11m
13. Liquids, Solids & Intermolecular Forces
Face Centered Cubic Unit Cell
Struggling with General Chemistry?
Join thousands of students who trust us to help them ace their exams!Watch the first video
Face Centered Cubic Unit Cell
Jules Bruno
Video duration:
1mPlay a video:
Related Videos
Related Practice