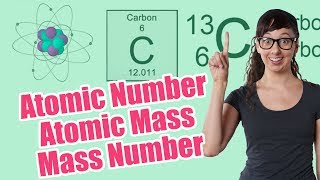Ch.2 - Atoms & Elements
Chapter 2, Problem 116
Boron has only two naturally occurring isotopes. The mass of boron-10 is 10.01294 amu and the mass of boron-11 is 11.00931 amu. Calculate the relative abundances of the two isotopes.
Verified Solution
Video duration:
0m:0s
This video solution was recommended by our tutors as helpful for the problem above.10087
views
Was this helpful?