Quantum mechanics is a fundamental area of physics that explores the behavior of very small particles, such as electrons, which can exhibit both particle-like and wave-like properties. This duality introduces complexities in determining the precise location and movement of these particles. A key principle in quantum mechanics is the Heisenberg uncertainty principle, which asserts that it is impossible to simultaneously know both the speed and position of an electron. Consequently, scientists focus on the probability of finding an electron in a particular location rather than its exact position.
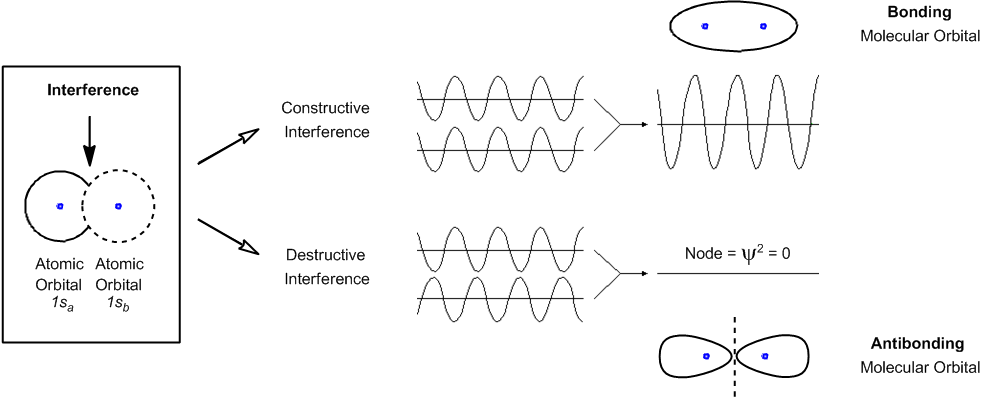
Wave functions, denoted by the symbol Ψ (Psi), are mathematical functions that describe the energy state of an electron. The probability of locating an electron can be derived from the wave function by squaring it, represented as |Ψ|². This squared value provides a three-dimensional plot known as an atomic orbital, which indicates the probable locations of electrons around the nucleus of an atom.
In chemistry, different types of atomic orbitals are recognized, including s and p orbitals. S orbitals are spherical, while p orbitals have a dumbbell shape, which can be remembered by associating them with the shape of peanuts. Each type of orbital is associated with specific energy levels. For example, in a carbon atom, which has an atomic number of 6, the electron configuration is 1s² 2s² 2p². This configuration indicates that carbon has six electrons distributed across its orbitals.
When filling the orbitals, the Pauli exclusion principle states that each orbital can hold a maximum of two electrons with opposite spins. Following the Aufbau principle, electrons fill lower energy orbitals before moving to higher ones. For carbon, the 1s orbital is filled first, followed by the 2s orbital. The 2p orbitals, which consist of three degenerate orbitals (2px, 2py, and 2pz), are filled according to Hund's rule, which suggests that each orbital should be half-filled before any orbital is fully filled. This results in a stable arrangement of electrons.
In summary, quantum mechanics provides a framework for understanding the behavior of electrons, emphasizing the probabilistic nature of their locations through wave functions and atomic orbitals. The concepts of uncertainty, probability, and electron configurations are essential for grasping the complexities of atomic structure and behavior.